Chapter Four: Classification
Applied Problems
A complete python script for each problem can be found in the current folder.
BASE_DIR = os.path.dirname(os.path.dirname(os.path.abspath(__file__)))
DATA_DIR = os.path.join(BASE_DIR, 'Data')
IMAGE_DIR = os.path.join(os.path.join(BASE_DIR, 'Images'), 'Chapter4')
Problem 10
Part a)
Load the data:
weekly_df = pd.read_csv(os.path.join(DATA_DIR, 'weekly.csv'))
An excerpt of the data is:
Year Lag1 Lag2 Lag3 Lag4 Lag5 Volume Today Direction
0 1990 0.816 1.572 -3.936 -0.229 -3.484 0.154976 -0.270 Down
1 1990 -0.270 0.816 1.572 -3.936 -0.229 0.148574 -2.576 Down
2 1990 -2.576 -0.270 0.816 1.572 -3.936 0.159837 3.514 Up
3 1990 3.514 -2.576 -0.270 0.816 1.572 0.161630 0.712 Up
4 1990 0.712 3.514 -2.576 -0.270 0.816 0.153728 1.178 Up
The info of the dataframe is:
0 Year 1089 non-null int64
1 Lag1 1089 non-null float64
2 Lag2 1089 non-null float64
3 Lag3 1089 non-null float64
4 Lag4 1089 non-null float64
5 Lag5 1089 non-null float64
6 Volume 1089 non-null float64
7 Today 1089 non-null float64
8 Direction 1089 non-null object
There are 7 numerical columns and a single categorical column.
From the pairplot of the numeric data we can make the following conclusions:
- Apart from 'Volume' and 'Year' the variables are normally distributed. Therefor using LDA or QDA will be an appropriate method for classification.
- 'Year' of course is not linear distributed and shoudl represent a uniform distribution assuming the same amount of data was collected in each year. The KDE plots do not drop off at the beginning and end of the sample collection as espected. This is due to the process of how KDE is calculated and the tails from each of the datpoints results in the smooth drop-off we see.
- From the pariplot the univariate distribution of 'Volume' is skewed to the left. This may be a logarithmic distribution. This is reenforced by the exponential trend of the scatter between the 'Year' plot with should be equally spaced intervals.
- Other than 'year' and 'volume' there appears to be no pattern between the values.
- Comaparing the distributions of the 'Direction' variables from the hues we can see that there is no discernible pattern separating the two classes. This will make it very difficult to classify the trajectory given these varaibles.
To test our suspicion of the distribution of 'Volume' we take its logarithm and replot the KDE.
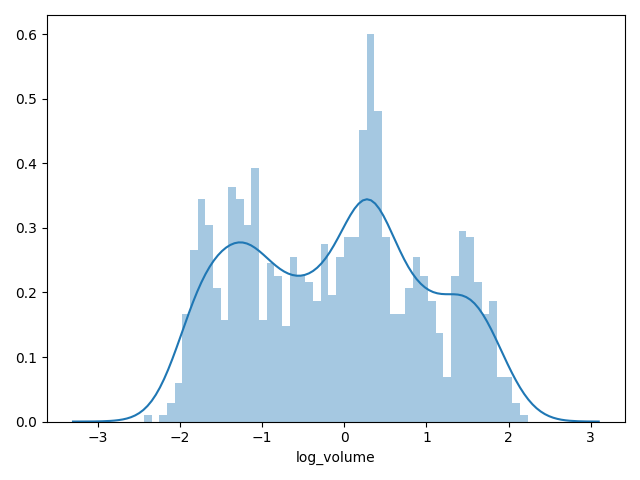
To see the difference between 'Direction' and the numerical variables we produce a series of box plots for the two categories:
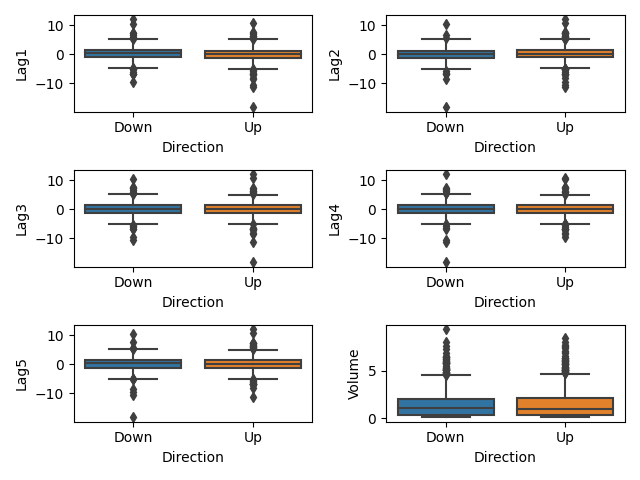
We see that in all of the numerical variable there is no discernible separation between the two classes for any of the variables. This makes it seem unlikely that any of these varaibles will be good enough to train a classification model on.
Finally we look at the scatter plots of the binarized 'Direction' variable and attempt to fit a logarithm to it:
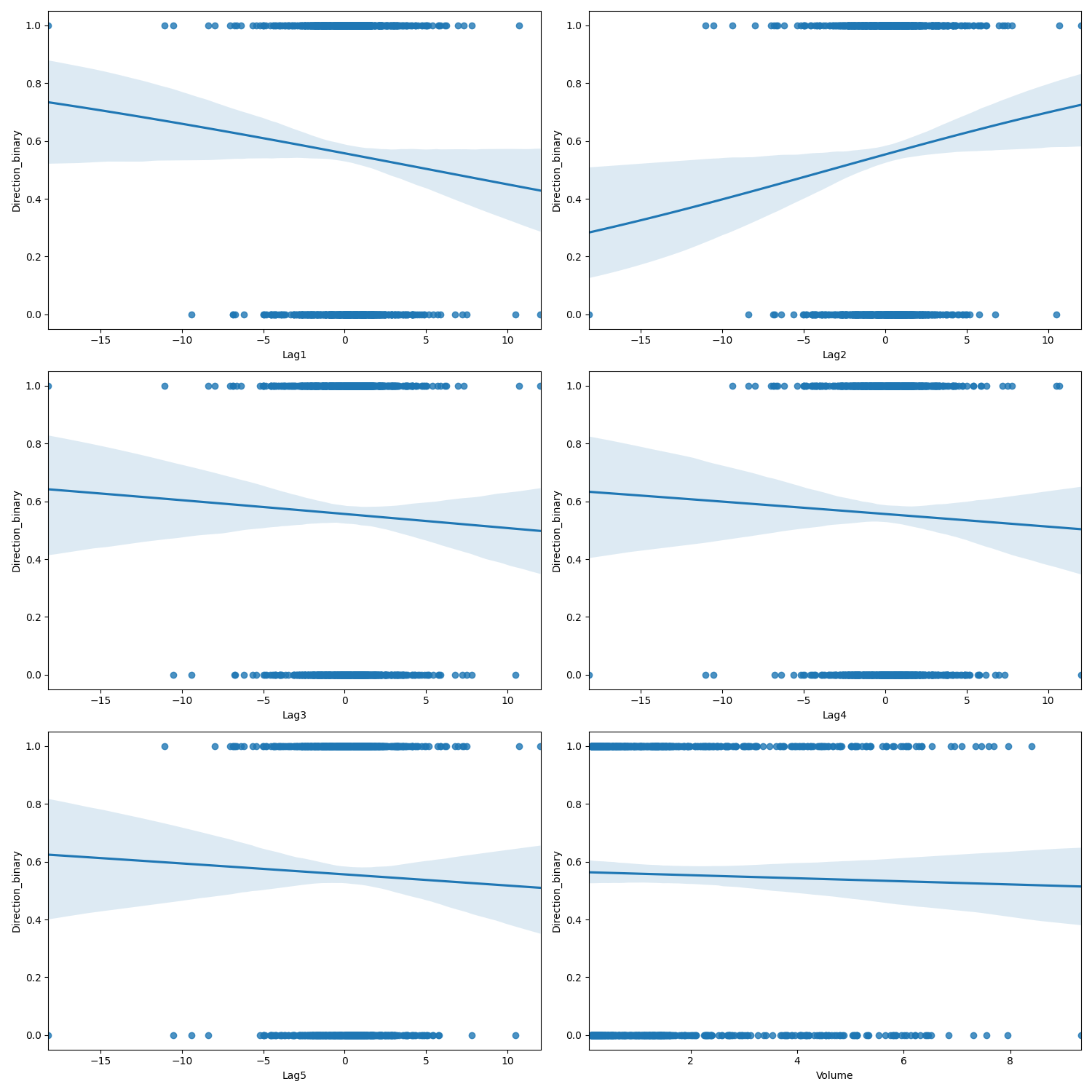
These scatterplots confirm our fears... this data lacks any sort of logarithmic relationship as none of the plots have an S-curve shape. The closest is for Lag2.
Part b)
Logit Regression Results
==============================================================================
Dep. Variable: Direction No. Observations: 1089
Model: Logit Df Residuals: 1082
Method: MLE Df Model: 6
Date: Sun, 29 Mar 2020 Pseudo R-squ.: 0.006580
Time: 18:10:38 Log-Likelihood: -743.18
converged: True LL-Null: -748.10
Covariance Type: nonrobust LLR p-value: 0.1313
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.2669 0.086 3.106 0.002 0.098 0.435
Volume -0.0227 0.037 -0.616 0.538 -0.095 0.050
Lag1 -0.0413 0.026 -1.563 0.118 -0.093 0.010
Lag2 0.0584 0.027 2.175 0.030 0.006 0.111
Lag3 -0.0161 0.027 -0.602 0.547 -0.068 0.036
Lag4 -0.0278 0.026 -1.050 0.294 -0.080 0.024
Lag5 -0.0145 0.026 -0.549 0.583 -0.066 0.037
==============================================================================
From the results of the Logistic regression we can see that the p-values for all the numeric varaibles are quite high. The lowest, and closest to being statistically significant is 'Lag2' with a p-value of 0.03. The positive coefficient for this lag suggests that a postive return for the stock market two days ago means an increase in the stock today. These results agree with our suspicions from the plot inspections.
Part c)
Confusion matrix using the logistic fit and a threshold of 0.5 to classify the predictions. It should be noted that this is a poor way to implement the model as we are testing the model on the exact same data used to train it. This however, is still insufficient to produce good results. The confusion matrix of the predictions is:
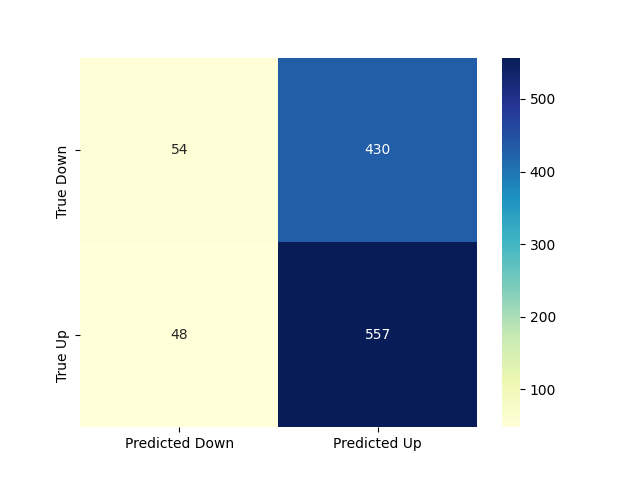
The elements of the confusion matrix correspond to:
True Negatives (Downs): Correct number of 'Down's predicted
True Positives (Ups): Correct number of 'Up's predicted
False Negatives(Downs): Number of 'Up's wrongly classified as 'Down's
False Positives (Ups): Number of 'Down's wrongly classified as 'Up's
The accuracy of these predictions are 56%. This is a terrible score, not much better than randomly guessing. This is to be expected as the variables did not have a logarithmic shape.
Parts d)-g)
Consider only the effect of 'Lag2' variable we perform each classification method. In this case we also split up the training and test cases as we train on 'historical data' and try and predict current data.
The results logistic regression results from part d) are:
Logit Regression Results
==============================================================================
Dep. Variable: Direction_binary No. Observations: 985
Model: Logit Df Residuals: 983
Method: MLE Df Model: 1
Date: Mon, 30 Mar 2020 Pseudo R-squ.: 0.003076
Time: 18:53:00 Log-Likelihood: -675.27
converged: True LL-Null: -677.35
Covariance Type: nonrobust LLR p-value: 0.04123
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 0.2033 0.064 3.162 0.002 0.077 0.329
Lag2 0.0581 0.029 2.024 0.043 0.002 0.114
==============================================================================
Rather than compute a confusion matrix for each plot we just present a table for each of the cases.
| Model | True Negatives | True Positives | False Negatives | False Posititives | Accuracy (%) |
|---|---|---|---|---|---|
| Logistic Reg. | 9 | 56 | 5 | 34 | 62 |
| LDA | 9 | 56 | 5 | 34 | 62 |
| QDA | 0 | 61 | 0 | 43 | 59 |
| KNN (N=1) | 21 | 30 | 31 | 22 | 49 |
h)
It is difficult to compare the performance of the models as they are all particularly poor at predicting the results. As the number of 'Up's and 'Down's is roughly the same in the data set and there is no particular reason to minimize the number of FPs or FNs specifically. Accuracy is a reasonable metric for this problem (unlike a disease for example). The highest accuray comes from the LDA and Logistic Regression with KNN being worse than guessing. Interestingly, the QDA model resulted in a particularly bullish strategy of assuming every day is an 'Up'.
In conclusion there is no model which can predict much better than random guessing using this data.
Problem 11
This problem is similar to 10 except using the 'auto' dataset to predict whether a can has above median mpg.
Part a)
Use the following code to generate the binary variable for mpg
auto_df = pd.read_csv(os.path.join(DATA_DIR, 'auto.csv'))
median_mpg = auto_df['mpg'].describe()['50%']
auto_df['mpg01'] = auto_df['mpg'].apply(lambda x: 1 if x > median_mpg else 0)
Part b)
We produced boxplots, distribution plots and scatter plots to analyze the data:
Boxplots
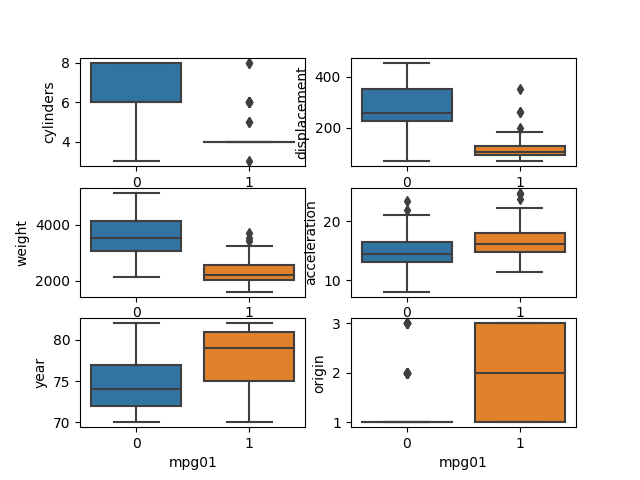
The Boxplots shows that there are statistical differences between the new categorical variable and the continous variables. For the Cylinder boxplot and the cars over the median results. There is a clear difference seen in the weights and the displacement plots. As the cylinders and orgin varaibles do not have a continous distribution function not much can be concluded about these varaibles from the boxplot.
Distribution plots
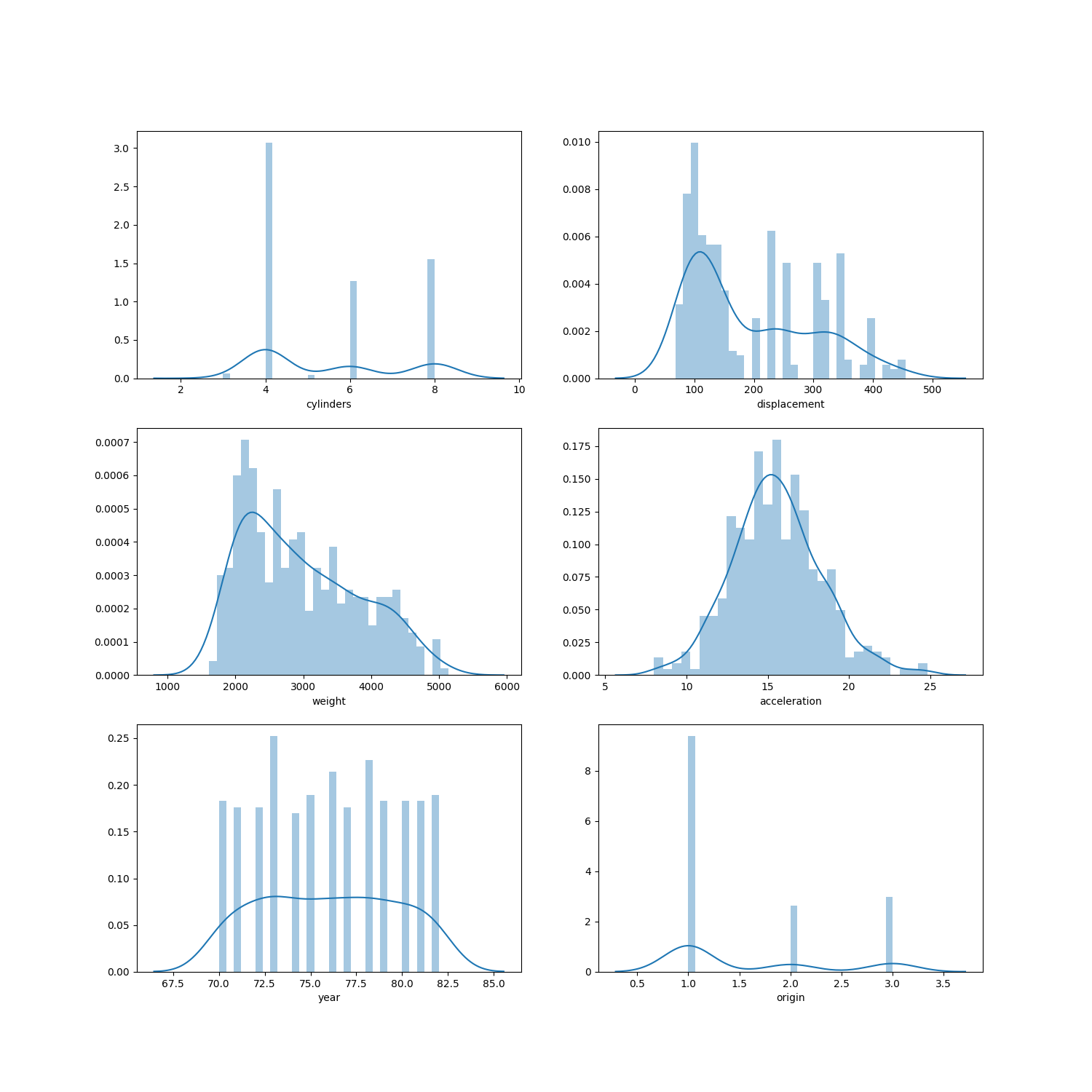
This shows the distribution of the continous variables. This is important as some of the classifications we consider are based on assumptions of normally distributed and continous predictors. From these plots we see that while acceleration seems to be normally distributed, the other variables do not. Therefore discriminant analysis techniques using these varaibles will be ineffective and could worsen the results.
Scatter plots
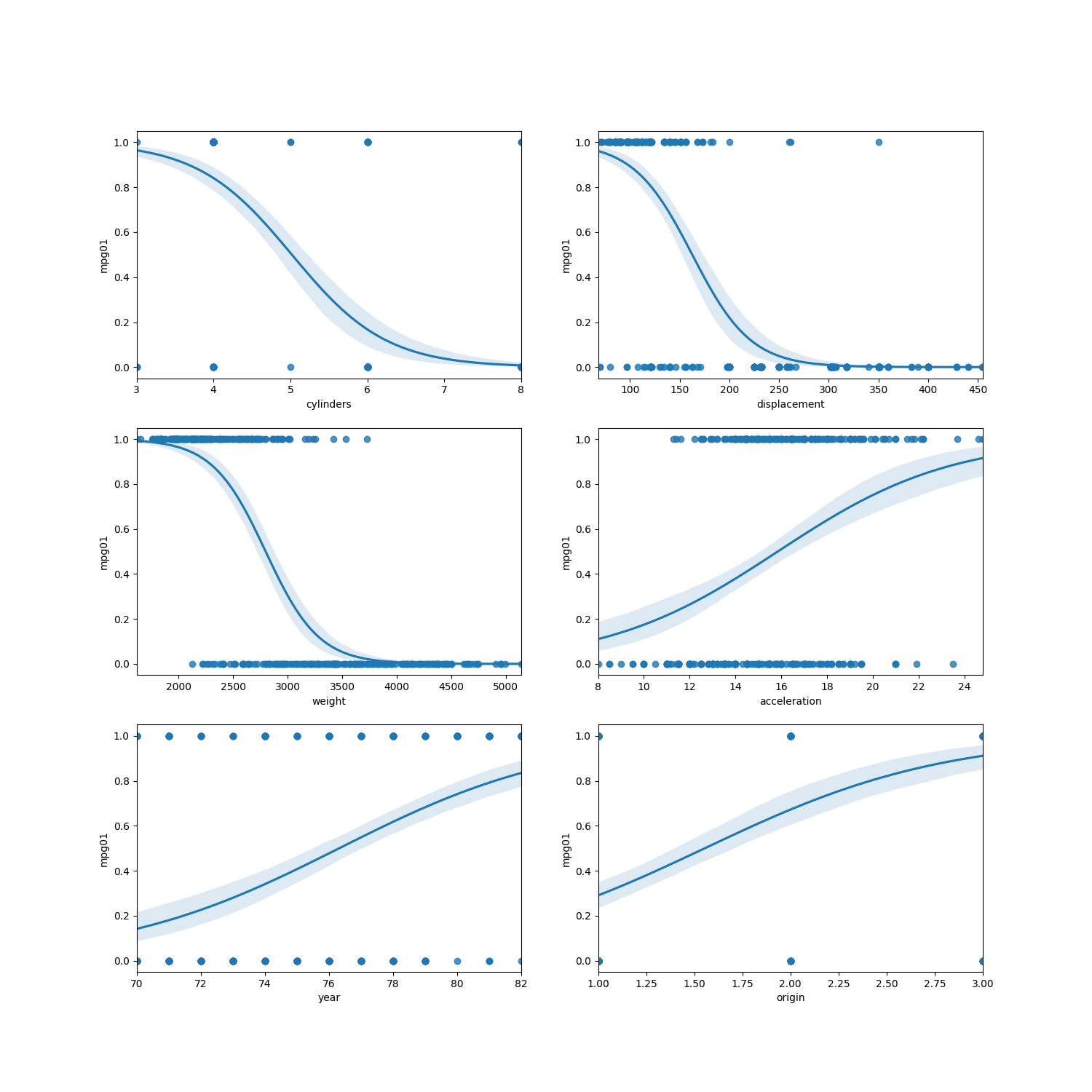
Lastly we have the scatter plots of the varaible with a logarithmic fit (see code for details). From these plots we can see that many of the varaible could be used for logistic regression.
From these plots we will use the varaibles weight, acceleration, displacement and cylinders as the predictor variables.
Part c)
Split the data with the following code. As there a similar number of each type (0, 1) in the dataset we do not have the problem of class imbalance. Therefore a simple random split of the data should be sufficient.
auto_df = pd.read_csv(os.path.join(DATA_DIR, 'auto.csv'))
median_mpg = auto_df['mpg'].describe()['50%']
auto_df['mpg01'] = auto_df['mpg'].apply(lambda x: 1 if x > median_mpg else 0)
print(auto_df.info())
print(auto_df.describe())
print(auto_df.columns)
print(auto_df['mpg01'].value_counts())
X_train, X_test, y_train, y_test = train_test_split(auto_df[['cylinders',
'displacement', 'weight', 'acceleration', 'year', 'origin']],
auto_df['mpg01'], test_size=0.2, random_state=1)
print(y_train.value_counts())
Parts d)-f) Classification with difference models
LDA
lda_model = LinearDiscriminantAnalysis()
lda_model.fit(X_train[['cylinders', 'displacement', 'weight', 'acceleration']], y_train)
preds = lda_model.predict(X_test[['cylinders', 'displacement', 'weight', 'acceleration']])
cm = confusion_matrix(y_test, preds)
tn, fp, fn, tp = confusion_matrix(y_test, preds).ravel()
LDA results:
True Negatives(TN) = 35
True Positives(TP) = 39
False Negatives(FN) = 1
False Positives (FN) = 5
Accuracy = 0.92
QDA
qda_model = QuadraticDiscriminantAnalysis()
qda_model.fit(X_train[['cylinders', 'displacement', 'weight', 'acceleration']], y_train)
preds = qda_model.predict(X_test[['cylinders', 'displacement', 'weight', 'acceleration']])
cm = confusion_matrix(y_test, preds)
QDA results:
True Negatives(TN) = 37
True Positives(TP) = 34
False Negatives(FN) = 6
False Positives (FN) = 3
Accuracy = 0.89
Logistic Regression (0.5 threshold)
First write a classifier function with a threshold for the output of the logistic regression
def classifier(value, threshold):
if value >= threshold:
return 1
else:
return 0
log_reg_results = smf.logit(formula = "mpg01 ~ cylinders + displacement + weight + acceleration", data= auto_df).fit()
print(log_reg_results.summary())
preds = log_reg_results.predict(X_test[['cylinders', 'displacement', 'weight', 'acceleration', 'year', 'origin']])
preds = preds.apply(lambda x: classifier(x, 0.5))
cm = confusion_matrix(y_test, preds)
Logistic regression results:
Logit Regression Results
==============================================================================
Dep. Variable: mpg01 No. Observations: 397
Model: Logit Df Residuals: 392
Method: MLE Df Model: 4
Date: Mon, 30 Mar 2020 Pseudo R-squ.: 0.5905
Time: 20:57:09 Log-Likelihood: -112.57
converged: True LL-Null: -274.90
Covariance Type: nonrobust LLR p-value: 5.192e-69
================================================================================
coef std err z P>|z| [0.025 0.975]
--------------------------------------------------------------------------------
Intercept 8.5851 1.759 4.880 0.000 5.137 12.033
cylinders -0.1324 0.327 -0.405 0.686 -0.774 0.509
displacement -0.0122 0.008 -1.517 0.129 -0.028 0.004
weight -0.0026 0.001 -3.863 0.000 -0.004 -0.001
acceleration 0.0899 0.079 1.133 0.257 -0.066 0.245
================================================================================
True Negatives(TN) = 35
True Positives(TP) = 35
False Negatives(FN) = 5
False Positives (FN) = 5
Accuracy = 0.88
Part g) KNN classification
width=20
print("N".ljust(width) + "|" + "True negatives".ljust(width) + "|" + "True Positives".ljust(width) + "|" + "False Negatives".ljust(width) + "|"+ "False Positives".ljust(width) + "|" + "Accuracy".ljust(width))
print("------------------------------------------------------------------------------------")
tn = {}
fp = {}
fn = {}
tp = {}
for n in range(1,20):
knn = KNeighborsClassifier(n_neighbors=n)
knn.fit(X_train[['cylinders', 'displacement', 'weight', 'acceleration', 'year', 'origin']], y_train)
preds = knn.predict(X_test[['cylinders', 'displacement', 'weight', 'acceleration', 'year', 'origin']])
cm = confusion_matrix(y_test, preds)
tn[n], fp[n], fn[n], tp[n] = confusion_matrix(y_test, preds).ravel()
# print(cm)
print("{}|{}|{}|{}|{}".format(str(n).ljust(width),str(tn[n]).ljust(width), str(tp[n]).ljust(width), str(fn[n]).ljust(width), str(fp[n]).ljust(width)))
KNN results:
| N | True negatives | True Positives | False Negatives | False Positives | Accuracy |
|---|---|---|---|---|---|
| 1 | 36 | 33 | 7 | 4 | 0.86 |
| 2 | 37 | 32 | 8 | 3 | 0.86 |
| 3 | 37 | 36 | 4 | 3 | 0.91 |
| 4 | 38 | 33 | 7 | 2 | 0.89 |
| 5 | 36 | 34 | 6 | 4 | 0.88 |
| 6 | 38 | 33 | 7 | 2 | 0.89 |
| 7 | 36 | 35 | 5 | 4 | 0.89 |
| 8 | 38 | 35 | 5 | 2 | 0.91 |
| 9 | 36 | 36 | 4 | 4 | 0.9 |
| 10 | 36 | 36 | 4 | 4 | 0.9 |
| 11 | 35 | 37 | 3 | 5 | 0.9 |
| 12 | 36 | 36 | 4 | 4 | 0.9 |
| 13 | 35 | 36 | 4 | 5 | 0.89 |
| 14 | 36 | 36 | 4 | 4 | 0.9 |
| 15 | 36 | 36 | 4 | 4 | 0.9 |
| 16 | 37 | 35 | 5 | 3 | 0.9 |
| 17 | 34 | 36 | 4 | 6 | 0.88 |
| 18 | 36 | 36 | 4 | 4 | 0.9 |
| 19 | 35 | 37 | 3 | 5 | 0.9 |
While there is not a large difference in the accuracy for different number of neighbours, the best be classifiers are for N=3 and N=8.