Credit Card Fraud Detection
Dataset: https://www.kaggle.com/mlg-ulb/creditcardfraud/data
This dataset contains labeled records of authentic and fraudulent transactions for a month in September 2013. Due to the sensitive nature of this data, it has been thoroughly cleaning with the feature set containing principal components of the original data obtained through pricipal component analysis. The name of the bank has not even been disclosed.
Despite the opacity of the data, in fact because of it, this is in a interesting dataset to see how well we can predict fraudulent credit card activity with little domain knowledge. A description of the data is located in the Data directory of the repository. A downside of not having the preprocessed data is we do not know "exactly" what was done to the data.
Data Exploration
Load the standard libraries and load the data
import pandas as pd
import numpy as np
import os
import matplotlib.pyplot as plt
import seaborn as sns
BASE_DIR = os.path.dirname(os.path.dirname(os.path.abspath(__file__)))
DATA_DIR = os.path.join(BASE_DIR, 'Data')
## Load the data
full_df = pd.read_csv(os.path.join(DATA_DIR, 'creditcard.csv'))
The first thing to note in this data is there are no missing values. This can be seen with the following code (output omitted).
print(full_df.is_nan().sum())
Distributions
We will begin by separating the data into the two classes to see if there are any clear statistical differences between the two sets.
## Separate the classes
Fraud_df = full_df[full_df['Class'] == 1]
Auth_df = full_df[full_df['Class'] == 0]
## Print the statistics of the amounts
print("\nFradulent 'Amount' statistics:")
print(Fraud_df['Amount'].describe())
print("\nAuthentic 'Amount' statistics: ")
print(Auth_df['Amount'].describe())
Fradulent 'Amount' statistics:
count 492.000000
mean 122.211321
std 256.683288
min 0.000000
25% 1.000000
50% 9.250000
75% 105.890000
max 2125.870000
Name: Amount, dtype: float64
Authentic 'Amount' statistics:
count 284315.000000
mean 88.291022
std 250.105092
min 0.000000
25% 5.650000
50% 22.000000
75% 77.050000
max 25691.160000
Name: Amount, dtype: float64
This demonstrates the extreme class imbalance of this problem. Only $\approx 0.1\%$ of the transactions are fraudulent. Therefore we will have to be very careful with how we split the training set for cross validation and how we score our models. Interestingly, the averages of the two classes are different enough to be considered notable. This leads us to think that Amount may be a good predictor. To see this further we plot the distributions of the two classes.
fig, ((ax1, ax2)) = plt.subplots(nrows=1, ncols=2, figsize=(18,12))
## Row 1
sns.distplot(a=Fraud_df['Amount'],bins=100, rug=True, ax=ax1)
sns.distplot(a=Auth_df['Amount'], bins=100, rug=True, ax=ax2)
ax1.set_title("Fradulent Amount Distribution")
ax2.set_title("Authentic Amount Distribution")
ax1.set_xlabel("Amount ($)")
ax2.set_xlabel("Amount ($)")
plt.show()
These distributions are hard to understand as they are extremely skewed. Both could be the log normal distributions and we can take the natural log of the amounts and plot the new distributions.
As there are transactions with Amount=0 and the logarithm is undefined so we ignore these values. We will remove these datapoints for the model as they aren't a transaction.
## Create column of the log transform of the amount
Fraud_df['log_Amount'] = Fraud_df['Amount'].apply(lambda a: np.log(a) if a!=0 else np.nan)
Auth_df['log_Amount'] = Auth_df['Amount'].apply(lambda a: np.log(a) if a!=0 else np.nan)
fig, ((ax1, ax2)) = plt.subplots(nrows=1, ncols=2, figsize=(18,12))
## Row 1
sns.distplot(a=Fraud_df['log_Amount'],bins=100, rug=True, ax=ax1)
sns.distplot(a=Auth_df['log_Amount'], bins=100, rug=True, ax=ax2)
ax1.set_title("Fradulent Log Amount Distribution")
ax2.set_title("Authentic Log Amount Distribution")
ax1.set_xlabel("Log Amount")
ax2.set_xlabel("Log Amount")
plt.show()
These log distributions are easier to read. We see a roughly smooth, possibly bimodel distribution, for the authentic transactions. We see a similar but more smooth distribution for the fraudulent transaction distributions.
Time dependence
One of the available raw columns is the Time column. While this variable does not represent some absolute time (like the Unix epoch) it shows the relative time from the first recorded transaction. We can then find out the total time over which the data was taken,
## Print the values where the 'Time' is the lowest
smallest_time = full_df['Time'].min()
print('First observations')
print(full_df[full_df['Time'] == smallest_time][['Time', 'Amount', 'Class']])
## Print the values where 'Time' is the largest
largest_time = full_df['Time'].max()
print('last observations')
print(full_df[full_df['Time'] == largest_time][['Time', 'Amount', 'Class']])
## Find and print the total timeframe of the data in a markdown table format
delta_seconds = largest_time - smallest_time
delta_minutes = delta_seconds/60.0
delta_hours = delta_minutes/60.0
delta_days = delta_hours/24.0
delta_months = delta_hours/30.0
First observations
Time Amount Class
0 0.0 149.62 0
1 0.0 2.69 0
Last observations
Time Amount Class
284806 172792.0 217.0 0
| timeframe | |
|---|---|
| seconds | 172792 |
| minutes | 2879.87 |
| hours | 48.00 |
| days | 2.00 |
Therefore, this data was taken over the period of two days. Which means that within 48 hours there have been about 500 fraudulent transactions. This shows how important detecting these can be.
The time column of this data will not be very useful. If the dataset was collected over a longer time we could perhaps perform some feauture engineering or find a pattern in the fraudulent transactions but the space of 2 days is too short.
Also the time data has been rounded to the nearest second which would not represent the true precision of the transaction. This will also obsfucate the time dependent nature of the data.
Lastly, without having the absolute time of the transactions we cannot feature engineer new, possibly powerful, predictors such as Hour_of_day, Day_of_week etc. . This could reveal times when these fraudulent actions are more prevalent which our model would take into account.
PCA Component Dependence
We can now consider the PCA components and see if there is any clear dependence. Once again, we do lose quite a bit of information having just given the PCs of the data. For instance, even if we were going to PCA decomposition in our models regardless, we would still have each PCA's explanined varaince and could find a skree plot. However, we don't so we are limited.
Preprocessing
One of the benefits of the PCA decomposition of the dataset is that there are no missing values and therefore we do not need to build in any sophisticated imputation in out preprocessing. Also, we hope that the data was scaled with mean 0 and unit standard deviation before the PCA to prevent the magnitude of the different variables having a large effect.
To begin the only preprocessing we will do is remove the $0 transactions from the dataset and scale the Amount predictor such that it has mean 0 and unit standard deviation.
from sklearn.preprocessing import StandardScaler
## Remove 0$ transactions
processed_df = full_df.drop(full_df[full_df['Amount'] == 0].index)
## Scale the amount columns
scaler = StandardScaler()
proc_df[['Amount']] = scaler.fit_transform(proc_df[['Amount']])
Scoring the models
One of the most important part of developing a model is finding a fair and objective way of measuring its success and comparing it against other models. In all problems, especially in classification problems, the choice of metric is domain dependent.
We cannot score the results on a crude model of total accuracy,
$$ \text{Total Accuracy} = \dfrac{\text{True Positives} + \text{True Negatives}}{\text{Size of dataset}} $$
as it will score extremely well on a model where all transactions are classified as authentic due to the extremely large class imbalance.
In this problem we note the following:
- We want to detect as many fraudulent transactions as possible (high recall).
- While it is alright to have a small number of false positives (incorrectly flagged authentic transactions) we want to minimise this number as well. (high precision)
Recall is defined as
$$ \text{Recall} = \dfrac{\text{True positives}}{\text{True positives} + \text{False Negatives}} $$
which represents how many of the fraudulent transactions were identified.
Precision is defined as
$$ \text{Precision} = \dfrac{\text{True positives}}{\text{True positives} + \text{False Positives}} $$
which represents how many of the flagged transactions were actually fraudulent.
A good metric for these problems is to consider the area under the Recall-Precision curve (AURPC). The Recall-Precision curve represents the relationship between the two metrics depending on the threshold of classification for the binary classes.
We will develop a model which maximizes the area under this curve. A AURPC of one is for a model with perfect precision and recall, that is there is no tradeoff depending on the threshold. The larger the AURPC the better the model.
Modelling
This is a classification problem where we aim to classify the entries based on the the amount and principal components. In a realistic scenario it might be important to have a model with a reasonable degree of interpretability and therefore a parametric model such as logistic regression might be appropriate. However, as the PCA values have already stripped the data of any interpretability we do not need to consider it. We will try a supporty vector machine with a non-linear kernel and also decision tree approaches.
SVM approach
We will start by testing the performance of support vector machines (SVMs). These models are extremely flexible though have little interpretability. As we have little interpretability to begin with they are a good choice to start. A core component of an SVM is the kernel used to generate the classification line. In this problem we consider the linear kernel, polynomial kernel, and the radial basis function kernel.
As the original dataset is large and will take a long time to train, we will test each kernel on a small subset of the dataset. We will use the train_test_split module of sklearn to sample a smaller subset with the same ratio of classes
from sklearn.model_selection import train_test_split
## Use all the predictors except 'Time'
X = proc_df.drop(['Class', 'Time'], axis=1)
y = proc_df['Class']
## Split the dataset such that it has the same ratio of samples (stratify) in each class
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=101, train_size=5000, stratify=y)
## Test that the classes were split proportionally
orginal_class_split = proc_df['Class'].value_counts()[0]/len(proc_df)
training_class_split = y_train.value_counts()[0]/len(y_train)
test_class_split = y_test.value_counts()[0]/len(y_test)
print("Original split \t 0: {:.2f}%, 1: {:.2f}%".format(orginal_class_split*100, (1-orginal_class_split)*100))
print("training set split \t 0: {:.2f}%, 1: {:.2f}%".format(training_class_split*100, (1-training_class_split)*100))
print("test set split \t 0: {:.2f}%, 1: {:.2f}%".format(test_class_split*100, (1-test_class_split)*100))
Original split 0: 99.84%, 1: 0.16%
training set split 0: 99.84%, 1: 0.16%
test set split 0: 99.84%, 1: 0.16%
Linear Kernel
To start we will test the linear kernel SVM. The hyperparameter which governs the linear classifier is the cost value C. Here C represents how flexible the model is and how many values can be missclassified. For this kernel we will cross-validate the linear SVM using different values of C. This is done with the following function
from sklearn.model_selection import cross_validate
from sklearn.svm import SVC
from sklearn.metrics import average_precision_score
def plot_score_vs_param(model,X, y, para, param_values):
"""
Generates a dictionary of results from cross-validating a model over a set of parameter values. Uses average precision score in cross validation.
Keyword Arguments
model: model to be cross-validated
X: Array or dataframe of predictor values
y: Array of response values
para: parameter to iterate over
param_values: list of parameter values to iterate over
"""
## Set baseline score
best_score = 0
## Make crossvalidator scorer with average precision score
aps = make_scorer(average_precision_score)
## Set empty list for storing training and test scores
cv_score_test = []
cv_score_train = []
values = param_values
## Iterate over parameter and return best score and best parameter value
for val in values:
print(para + '_value: ' + str(val))
if para == 'C':
model.set_params(C=val)
if para == 'gamma':
model.set_params(gamma=val)
if para == 'degree':
model.set_params(degree=val)
scores = cross_validate(model, X, y, return_train_score=True, n_jobs=-1, scoring=aps)
print('test score: ', scores['test_score'].mean())
print('train score: ', scores['train_score'].mean())
cv_score_test.append(scores['test_score'].mean())
cv_score_train.append(scores['train_score'].mean())
## If the iteraction is the current best perfomer, save the parameters and model
if scores['test_score'].mean() > best_score:
best_score = scores['test_score'].mean()
model.fit(X,y)
best_model = model
best_value = val
print('Best value of cost (C): ', best_value)
print('Best test set score: ', round(best_score, 3))
results = {}
results['best_test_score'] = best_score
results['best_model'] = best_model
results['best_value'] = best_value
results['train_scores'] = cv_score_train
results['test_scores'] = cv_score_test
return results
Using this function we can plot the train-test score curve for the different values of C
## intantiate the SVM with linear kernel
svm = SVC(kernel='linear', max_iter=10000000)
## generate a list of C values to iterate over (different orders of magnitude)
C_values = [np.power(10.0,x) for x in np.arange(-7,7,1)]
## Generate the cv score dictionary
C_results = plot_score_vs_param(svm, X_train, y_train, para='C', param_values=C_values)
## Plot the curves
fig, ax = plt.subplots(nrows=1, ncols=1, figsize=(12,12))
ax.plot(C_values, C_results['test_scores'], label='test score')
ax.plot(C_values, C_results['train_scores'], label='train_score')
ax.set_xlabel('C')
ax.set_ylabel('Score')
ax.set_title('Model performance for C')
ax.legend(fontsize = 'large')
ax.set_xscale('log')
score_label = "Best Test Score: {:.2f}".format(C_results['best_test_score'])
ax.text(0.1, 0.9, ha='center', va='center', s=score_label , fontsize=12, transform=ax.transAxes)
plt.show()
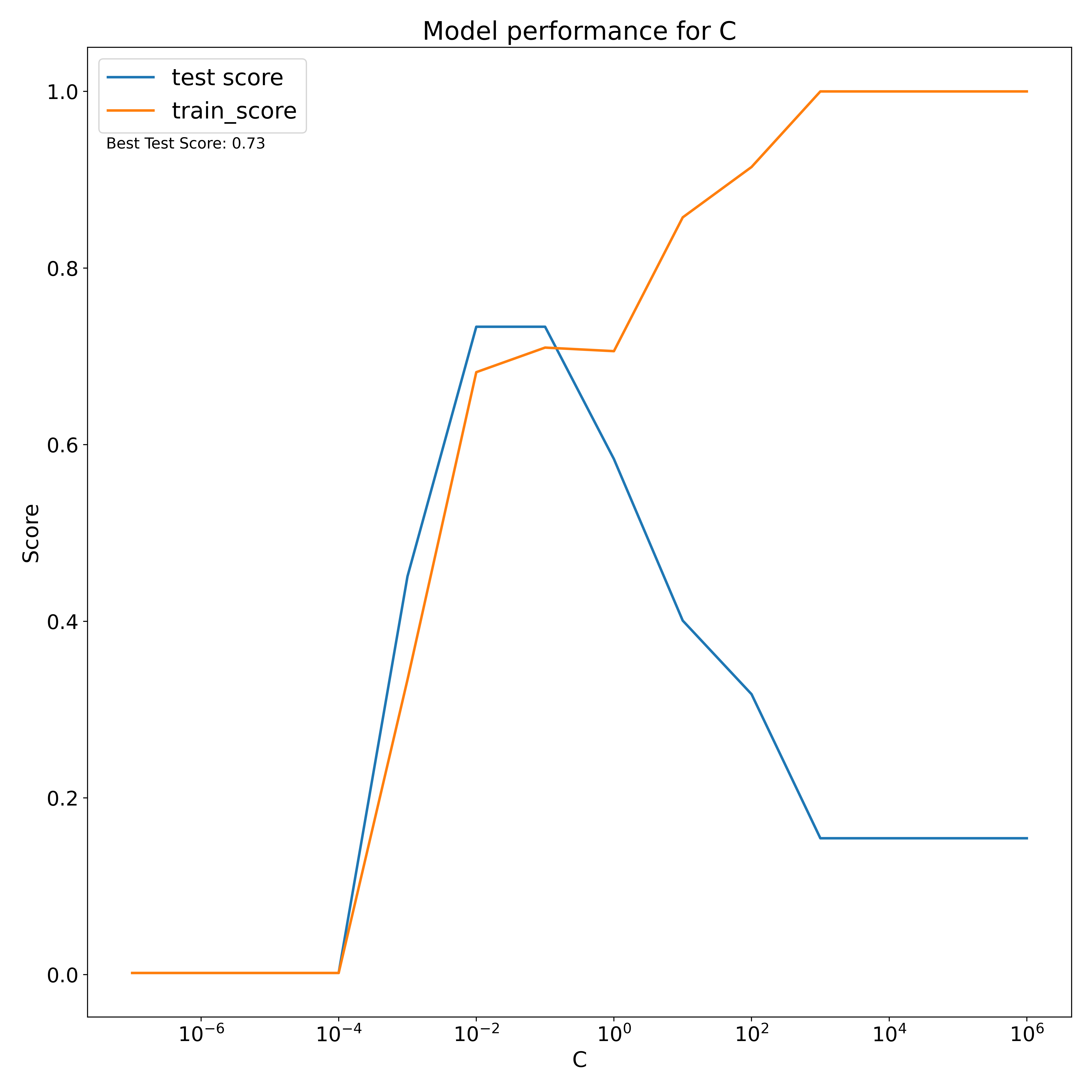
The linear kernel results in a best test score of 0.73 which, for an opaque dataset, is quite a reasonable model. This occurs for a cost value of C=0.1. This may vary when we train over the entire dataset.
Polynomial Kernel
Thy polynomial kernel, in comparsion to the linear kernel, has a large potential complexity. Compared to the single hyperparameter C in the linear kernel it has two in addition. The degree of polynomal for the decision boundary and gamma. Here gamma is a free parameter of the polynomial hyperline. It acts a scaling parameter to the decision boundary.
The larger the value of gamma, the larger the variance of the model and lower bias (opposite to C). Therefore, there is a fine interplay between these two hyperparameters. The best approach to optimizing these hyperparameters is either a randomized CV search (See this paper) or a standard grid search (this is feasible as we only have a grid of two hyperparameters to iterate over). However, as we are try to find the best model before our full hyperparameter optimization we use the crude method of finding the best hyperparameters independently.
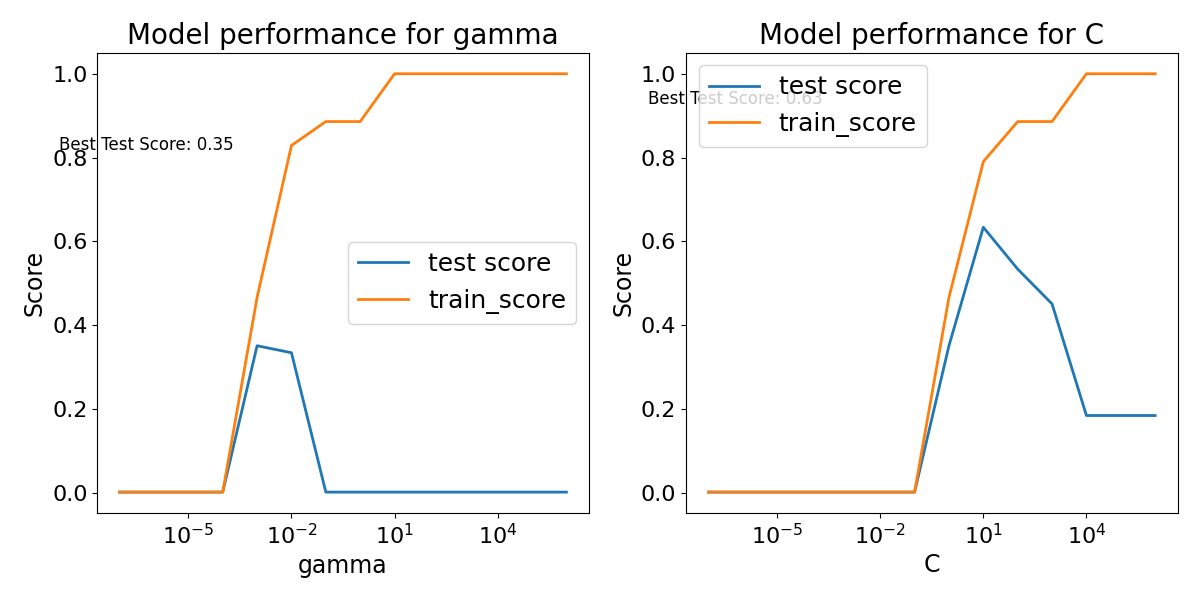
Below we iterate over the lowest 6 polynomial degrees and independently plot the CV scores for different gamma and C values.
## Instantiate the svc with polynomial kernel
svm = SVC(kernel='poly', C=0.1, max_iter=1000000)
## Create the list of polynomial degress to iterate over
degree_values = [1,2,3,4,5,6]
## Define grid of gamma values and C values
gamma_values = [np.power(10.0,x) for x in np.arange(-9,7,1)]
C_values = [np.power(10.0,x) for x in np.arange(-7,10,1)]
## Set up figure to plot train, test scores
fig, axs = plt.subplots(nrows=len(degree_values), ncols=2, figsize=(12,48))
plt.subplots_adjust(hspace=0.5)
## For each degree produce a new row in the plot
for idx, deg in enumerate(degree_values):
print("Degree: ", deg)
## Update model with new polynomial degree
svm.set_params(degree=deg)
## Perform CV with gamma values
gamma_results = plot_score_vs_param(svm, X_train, y_train, para='gamma', param_values=gamma_values)
## Update model with best gamma value
svm.set_params(gamma=gamma_results['best_value'])
## Perform CV with C values
C_results = plot_score_vs_param(svm, X_train, y_train, para='C', param_values=C_values)
## Update axes with new plots
axs[idx,0].plot(gamma_values, gamma_results['test_scores'], label='test score')
axs[idx,0].plot(gamma_values, gamma_results['train_scores'], label='train_score')
axs[idx,0].set_xlabel('gamma')
axs[idx,0].set_ylabel('Score')
axs[idx,0].set_title('Model performance for gamma (Degree {})'.format(deg))
axs[idx,0].legend(fontsize = 'large')
axs[idx,0].set_xscale('log')
score_label = "Best Test Score: {:.2f}".format(gamma_results['best_test_score'])
axs[idx,0].text(0.1, 0.9, ha='center', va='center', s=score_label , fontsize=12, transform=axs[idx,0].transAxes)
axs[idx,1].plot(C_values, C_results['test_scores'], label='test score')
axs[idx,1].plot(C_values, C_results['train_scores'], label='train_score')
axs[idx,1].set_xlabel('C')
axs[idx,1].set_ylabel('Score')
axs[idx,1].set_title('Model performance for C (Degree: {0}, gamma: {1:.2})'.format(deg,gamma_results['best_value']))
score_label = "Best Test Score: {:.2f}".format(C_results['best_test_score'])
axs[idx,1].text(0.1, 0.9, ha='center', va='center', s=score_label , fontsize=12, transform=axs[idx,1].transAxes)
axs[idx,1].legend(fontsize = 'large')
axs[idx,1].set_xscale('log')
plt.show()
Here Degree=1 is the linear decision boundary exactly. Surprisingly, it also still has the largest the best score. Therefore the more complex decision boundary did not improve the results.
Radial Kernel
The radial basis function kernel, like the polynomial kernel, has two hyperparameters. Therefore we do the same cv score plots as the polynomial kernel.